NCEA Level 2 Mathematics, Algebra Exam 2019
Exam held on Thursday 21 November 2019.
algebra mistake, TWO (d) | algebra ONE (c) | algebra TWO (e)
QUESTION TWO (d), Algebra exam mistake
This mistake was bad enought to be mentioned in this NZ Herald article (sadly now behind a paywall).
Basically, a rectangle is divided into two areas. The shaded rectangle – which fits completely inside the larger rectangle – has an area of 9 cm2. A diagram is given with some dimensions. Find the area of the larger rectangle.

Radio NZ posted a couple of videos here and here with University of Auckland's Padraic Bartlett explaining the problem. Sadly the maths professor has very messy writing.
`y(y - 8) = 9`
`y^2 - 8y - 9 = 0`
`(y - 9)(y + 1) = 0`
`y = 9 or y = -1`
It's a rectangle, so y must be positive, hence y = 9. The shaded rectangle is thus 1 cm wide and 9 cm tall.
`x = y - 8 + y + 2`
`x = 2y - 6`
`x = 2(9) - 6`
`x = 18 - 6`
`x = 12` (rectangle width)
`x - 4 = 8` (rectangle height)
Hence the larger rectangle is 12 cm wide and 8 cm tall. But the height of the shaded rectangle is 9 cm. That means the distance from the bottom of the shaded rectangle to the bottom of the larger rectangle is -1 cm!
But anyway, the question still needs to be finished. After getting a result for a calculation, reread the question and use your calculation result accordingly.
large rectangle area `= 12 × 8 = 96 cm^2`
Comment:
It's incredible that mistakes are still making it through the NCEA exam preparation process. Hasn't NZQA learned anything!? It's been making mistakes for years!
As has been pointed out elsewhere, the area of the rectangle can be found even with the mistake, but the mistake is a trap for more capable students, since they are more likely to check their answer and find it cannot possibly be right, which could lead to them wasting a lot of time trying to figure out where they went wrong. It's a maths exam, not a psychology experiment!
I don't see any problem with the way the rectangle is labelled. Students should be aware they need to be careful in what they are doing, and what they are using. The marking scheme should allow for the relative importance of using the wrong dimension.
Update: The official comment from NZQA was along the lines of the question is OK since the problem would only be found by the few people who tried to apply their answers back to the diagram – obviously something NONE of the checkers tried! – so it's not a problem. I would say it's actually something that anyone with even a semi-decent number memory would instantly notice after calculating the height of the large rectangle.
QUESTION ONE (c)
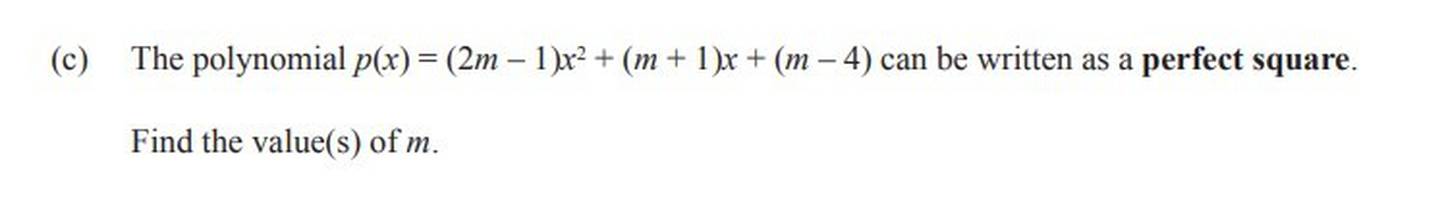
If p(x) is a perfect square then it will only have one repeated root, which means the discriminant equals zero. This allows us to make an equation which can be solved.
`b^2 - 4ac = 0`
`(m + 1)^2 - 4(2m - 1)(m - 4) = 0`
`(m^2 + 2m + 1) - 4(2m^2 - 9m + 4) = 0`
`m^2 + 2m + 1 - 8m^2 + 36m - 16 = 0`
`-7m^2 + 38m - 15 = 0`
Now use the quadratic formula or hope the answer is a whole number and try to factorise.
`m = (-38 ± sqrt(38^2 - 4(-7)(-15)))/ -14`
`m = (-38 ± sqrt(1024) )/ -14`
`m = (-38 ± 32) / -14`
`m = (-6)/-14 = 3/7`
or `m = (-70)/-14 = 5` |
|
Factorising will be easier with a positive x2 term.
`7m^2 - 38m + 15 = 0`
7 is a prime number which only factorises one way (with integers). The + sign on the 15 tells us the signs in the factors are the same, and the - sign on the 38m tells us they're both negative.
`(7m - A)(m - B) = 0`
Ignoring the negative signs for the moment, we're looking for two numbers which multiply to 15 and (after one is multiplied by 7) have a sum of 38. (We don't need to continue checking the options after we find the sum we're looking for.)
A
|
B
(x7 toward
the sum) |
Sum |
| 1 |
15 |
106 |
| 3 |
5 |
38 |
| 5 |
3 |
26 |
| 15 |
1 |
22 |
`(7m - 3)(m - 5) = 0`
`7m - 3 = 0`
`m = 3/7`
or `m - 5 = 0`
`m = 5` |
But wait. We set the discriminant equal to zero because a perfect square means we were looking for a single root, and yet we (apparently) have two possible values of m. This implies there are two possible perfect squares. Are there really two, or did we introduce a phantom solution when we used b2 in the discriminant?
We need to test our solutions.
Update: The marking schedule points out that the constant term in the original polynomial must be positive for a perfect square, meaning that m - 4 > 0. This rules out m = 3/7 as a solution.
An alternate (much more time consuming) method to rule out m = 3/7 involves testing both possible solutions and finding that m = 3/7 does not actually give a perfect square (unless complex numbers are invoked, which are only introduced in NCEA Level 3).
`(2m - 1)x^2 + (m + 1)x + (m - 4)`
`= (2(3/7) – 1)x^2 + ((3/7) + 1)x + ((3/7) – 4)`
`= -1/7x^2 +10/7x - 25/7`
`= -1/7(x^2 + 10x - 25)`
`= -1/7(x – 5)^2`
Not a perfect square!
(Complex numbers are not in NCEA 2.)
`(2(5) - 1)x^2 + ((5) + 1)x + ((5) - 4)`
`= 9x^2 + 6x + 1`
`= (3x + 1)^2`
Perfect square!
We therefore reject 3/7 as a solution and conclude that m = 5 (only).
QUESTION TWO (e)
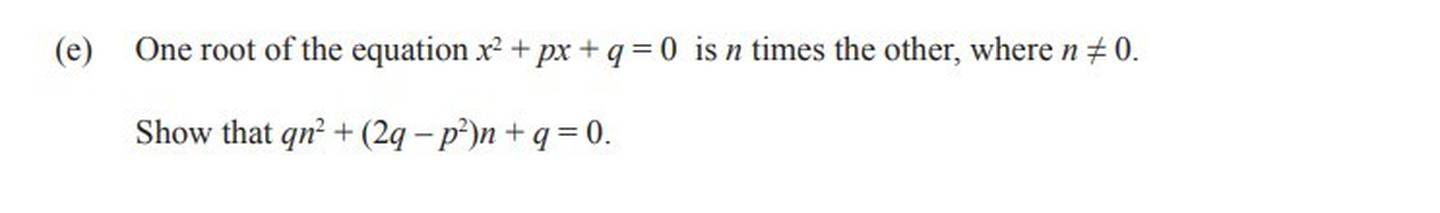
First factorise with a placeholder, a. We'll get rid of it later. Expand and form expressions for p and q from the given quadratic.
`(x + a)(x + an) = 0`
`x^2 + anx + ax + a^2n = 0`
`x^2 + a(n + 1)x + a^2n = 0`
Comparing this with the original equation, we can form expressions for p and q, then rearrange to get expressions for a and a2.
`x^2 + a(n + 1)x + a^2n = 0`
`x^2 + px + q = 0`
| |
`p = a(n + 1)`
`a = p / (n + 1)` |
`q = a^2n`
`a^2= q / n` |
|
There are (at least) a couple of approaches from here.
EITHER
Make an equation by squaring the first one (with p), letting them equal each other to remove a, then rearrange.
`p^2 / (n + 1)^2 = q / n`
`p^2n = q(n + 1)^2`
`p^2n = q(n^2 + 2n + 1)`
`p^2n = qn^2 + 2qn + q`
`qn^2 + 2qn - p^2n + q = 0`
`qn^2 + (2q - p^2)n + q = 0`
That's quite efficient, but it's not necessarily obvious why making the equation is a good idea. Basically, we should try it because we want an equation with `n`, `p`, and `q`. This does, so try it and see if it gives anything useful. In other words, throw stuff together and see what sticks. |
|
OR
Substitute the two roots into x in the original equation, then replace a and a2 with their equal expressions.
`x^2 + px + q = 0`
First one root:
`(-a)^2+ p(-a) + q = 0`
`a^2 - ap + q = 0`
`q / n - (p / (n + 1))p + q = 0`
`q / n - p^2 / (n + 1) + q = 0`
Then the other root:
`(-an)^2 + p(-an) + q = 0`
`a^2n^2 - apn + q = 0`
`(q / n)n^2 - (p / (n + 1))pn + q = 0`
`qn - (p^2n) / (n + 1) + q = 0`
Start rearranging. Note that the first result can be changed into the second simply by multiplying by n.
`q / n - p^2 / (n + 1) + q = 0`
`q - (p^2n) / (n + 1) + qn = 0`
Get rid of the denominator by multiplying by n+1, expand, rearrange to a quadratic in n.
`q(n + 1) - p^2n + qn(n + 1) = 0`
`qn + q - p^2n + qn^2 + qn = 0`
`qn^2 + 2qn - p^2n + q = 0`
`qn^2 + (2q - p^2)n + q = 0` |
Comment:
I found this one quite tricky and really had to think to figure out how to get an equation that could be manipulated into the required form. The maths itself is pretty straight-forward. The question will likely show which students really know how to apply what they know.
Update:
The method in the assessment schedule is different again, and I've been asked by one of my students to explain it; there just wasn't enough given in the assessment schedule to follow. It'll certainly be easier to understand with a few more lines of working than the assessment schedule gives.
To start, the equation's two roots can be found with the quadratic formula.
`x^2 + px + q = 0`
`x = (-p ± sqrt(p^2 - 4q))/2`
The larger of these roots is n times the smaller, so they can be equated by throwing in a factor of n on one side of the equation (it doesn't matter which side). Then get rid of the denominators.
`(-p + sqrt(p^2 - 4q))/2 = (n(-p - sqrt(p^2 - 4q)))/2`
`-p + sqrt(p^2 - 4q) = n(-p - sqrt(p^2 - 4q))`
We want to get rid of the square roots, so rearrange so the square roots are on the same side.
`-p + sqrt(p^2 - 4q) = -pn - nsqrt(p^2 - 4q)`
`sqrt(p^2 - 4q) + nsqrt(p^2 - 4q)= p - pn`
Factorise to be able to get just one square root. Then get rid of it by squaring everything.
`(1 + n)(sqrt(p^2 - 4q))= p(1 - n)`
`sqrt(p^2 - 4q) = (p(1 - n))/(1 + n)`
`p^2 - 4q = ((p(1 - n))/(1 + n))^2`
`p^2 - 4q = (p^2(1 - n)^2)/(1 + n)^2`
Again, get rid of the denominator, then expand.
`(1 + n)^2(p^2 - 4q) = p^2(1 - n)^2`
`(1 + 2n + n^2)(p^2 - 4q) = p^2(1 - 2n +n^2)`
`(p^2 + 2p^2n + p^2n^2) - (4q + 8qn + 4qn^2) = p^2 - 2p^2n + p^2n^2`
`p^2 + 2p^2n + p^2n^2 - 4q - 8qn - 4qn^2 = p^2 - 2p^2n + p^2n^2`
Cancel terms which are on both sides, then shift everything to the left and take out a common factor of 4.
`2p^2n - 4q - 8qn - 4qn^2 = - 2p^2n`
`4p^2n - 4q - 8qn - 4qn^2 = 0`
`p^2n - q - 2qn - qn^2 = 0`
We want to make a quadratic in n, so we need to rearrange (including changing the sign of every term), then factorise to get the middle term.
`- p^2n + q + 2qn + qn^2 = 0`
`qn^2 + 2qn - p^2n + q = 0`
`qn^2 + (2q - p^2)n + q = 0`
And there we have it. "Just a few" lines of working missing from the assessment schedule – which has just three lines of working after stating the roots; the full working for that approach as I show above takes a full page and a half on my computer screen. No wonder my student wanted it explained. My first approach above is definitely more efficient.
Second comment:
Why would an NCEA Level 2 student try any of these three (or possible other) approaches? Blind guess? Wild hunch? Just trying stuff until something works? Is there some NCEA 2 principle that's being applied or shown here?
Two of the three approaches above take a lot of working, with the method used in the assessment schedule(!) being particularly lengthy and time consuming. I believe it is unreasonable to expect such a huge amount of working in a Level 2 exam, but that's the approach which the assessment schedule uses.
|

