Two possible configurations of a house shape drawn below a parabola are shown below.
A house shape is drawn as shown where:
- C is at (0,9).
- A and B are points on the parabola `y = 9 - x^2`.
- E and F are on the `x`-axis.
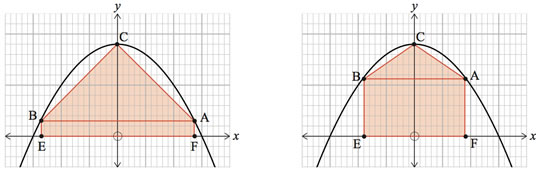
(i) Find the height of the wall (AF or BE) when the area of the house shape is a maximum. Justify that this is the maximum area.
Differentiate to find maximum area. We first need an expression for the area. There are two main approaches: treat it as a triangle and a rectangle; or treat it as two back-to-back trapeziums. If I use trapeziums I only need to calculate one area and double it.
Since A is a point I'll use HA to represent the house area. Draw a diagram to help yourself understand how the house shape works!
Area of trapezium `= (a+b)/2 times h`
House area `= HA = 2 times (a+b)/2 times h = h(a+b)`
`HA = x(9 + y)`
When substituting in, it's a good idea to use brackets. It helps prevent mistakes with negative signs cancelling, but it's a good habit to get into even when the negative signs will not cancel.
`HA = x(9 + (9 - x^2))`
`HA = x(18 - x^2)`
`HA = 18x - x^3`
And that's the expression we need for the area. Now we can differentiate and solve.
`(d(HA))/dx = 18 - 3x^2 = 0` at maximum house area
`3x^2 = 18`
`x^2 = 6`
`x = sqrt6`
I'm only interested in the positive value because the house shape is symmetrical about the `y`-axis.
After getting the result of a calculation, reread the question. This one is asking for the wall height, which is simply the `y` value at the calculated `x` value, and justification for the area with this wall height being a maximum.
`y = 9 - x^2`
The wall height at maximum area is `y = 9 - (sqrt6)^2 = 9 - 6 = 3`
`(d^2(HA))/dx^2 = -6x = -6(sqrt6) ≈ -14.70 < 0 =>` local maximum
Comment:
Part (i) is pretty straight-forward. Using an expression based on a triangle and rectangle gives the same expression for area but with a little more working to get there.
Other methods than the second derivative are also accepted for justifying it's a maximum, including the simple approach of pointing out that the second stationary point of a negative cubic is a local maximum.
Be very clear on what this question requires. It is not wanting the maximum area or any particular value to be calculated. The student needs to show that two areas are the same. This requires a clear idea of what to aim at, and clear working so the student and marker know what is going on throughout the proof process.
I'm going to be very thorough in my working for this question so that what's going on is as clear as possible, and make sure I'm not using information from part (i) that no longer applies.
We'll start by obtaining simplified expressions for the areas of the triangle and the rectangle. (This is when calculating the areas in part (i) would have been good to do with a triangle and rectangle. Not a worry, this is simple enough.) Start with a formula and substitute variables and expressions in as needed. Simplify as much as possible, reducing to just one variable (and the two constants).
If point A has coordinates `(x,y)` then the areas are:
`{:(A_"tri", =, 1/2bh), (,=, 1/2 times 2x(d - y)), (,=, x(d - y)), (,=, x(d - (d - kx^2))), (,=, x(d - d + kx^2)), (,=, x(kx^2)), (,=, kx^3):}`
(Note the usefulness of the brackets when substituting the expression for `y` into the `A_"tri"` formula above. It's a simple way to help avoid missing the cancellation of the two negative signs; make it a habit when substituting in.)
`{:(A_"rect", =, bh), (,=, 2xy), (, =, 2x(d - kx^2)), (, =, 2dx - 2kx^3):}`
These two expressions have some similarities and some differences. What special condition/s will occur at maximum area to make these equal? This is what we need to be asking ourselves as we go through the next step.
When maximum area occurs, the derivative of the total area will be zero. Even if it's for no better reason than "because this is a calculus question and we need to differentiate something", we'll take the total area and differentiate it. It will at least give us something to work with.
`{:(A_"total", =, A_"tri" + A_"rect"), (,=, kx^3 + 2dx - 2kx^3), (,=, 2dx - kx^3):}`
`(dA_"total")/dx = 2d - 3kx^2 = 0` at maximum area
`2d = 3kx^2`
At about this point it's good to wonder about what use this could be, since we can't actually solve for `x`. (Trying to rearrange it to an expression for `x` – like the assessment schedule and various YouTubers do – makes for a complicated and unwieldy expression that takes a lot of working, but does work eventually.)
The differential gives us an expression for 2d at maximum area in terms of `k` and `x`. The expression has some similarity with other terms, and it happens that we have an instance of 2d which would be very nice to get rid of...
`{:(A_"tri", =, kx^3), (A_"rect", =, 2dx - 2kx^3), (,=, (3kx^2)x - 2kx^3), (,=, 3kx^3 - 2kx^3), (,=, kx^3), (,=, A_"tri"):}`
`=>` At maximum area, the areas of the triangle and rectangle are equal.
QED
If you manage to prove something like what was asked for in this question, it's important to include the QED at the end. You are allowed to feel rightfully smug about this sort of achievement.
Wikipedia:
Q.E.D. or QED is an initialism of the Latin phrase quod erat demonstrandum, meaning "that which was to be demonstrated". Literally, it states "what was to be shown". Traditionally, the abbreviation is placed at the end of mathematical proofs and philosophical arguments in print publications, to indicate that the proof or the argument is complete.
Comment:
Part (ii) requires a clear idea of what the question requires, and clear working. If you're working towards a proof, not a particular value, you'll likely have to show that two expressions are equal to each other. If your working is very clear – clearly laid out, clearly labelled – then you'll be more likely to notice things such as being able to replace that `2d` term.
Also, the working in the assessment schedule is unnecessarily complicated. It seems to have somehow avoided any hint of the much simpler working I've given above. Why aren't the expressions for the individual areas simplified before summing? Seriously, how would anyone spot if they had equated the areas when using such complicated expressions? "With much more working, of course." But why make the working more difficult than it needs to be? (I acknowledge that for completeness the final expression in the schedule should be listed as an alternate expression for the proof.)

